Exponenciální a logaritmické funkce
Exponenciální funkce exp(x) vrací hodnotu ex pro reálná čísla x, e = 2.718 je základ přirozených logaritmů.
Tato konstanta má ve Scilabu definovanou hodnotu
Příklad 4.2.A - konstanta %e
%e
%e = 2.7182818
// nebo také e = exp(1)
e = exp(1)
e = 2.7182818
Příklad 4.2.B - výpočty - exponenciální funkce
// Výpočet e-2.3
exp(-2.3)
ans = 0.1002588
exp([-1 0 1 2 3])
ans =
0.3678794 1. 2.7182818 7.3890561 20.085537
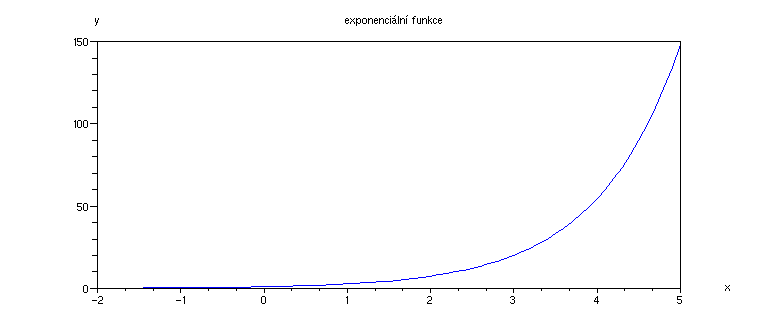
Graf exponenciální funkce:
Příklad 4.2.C - graf exponenciální funkce
x = [-2:0.1:5]; // definujeme obor hodnot x
plot(x,exp(x)); // graf
xtitle('exponenciální funkce','x','y') // popis grafu a os
Exponenciální funkci můžeme použít i u komplexních čísel s vyjádřením
exp(z) = ea+bi = ea ebi = ea (cos a +isin b) = ea cos a + eb isin b
Příklad 4.2.D - výpočet exponenciální funkce u komplexních čísel
exp(3+4*%i)
ans = - 13.128783 - 15.200784i
Inverzní funkce k exponenciální funkci je přirozený logaritmus ln (x).
Log
Ve Scilabu odpovídá přirozenému logaritmu funkce log(x).
Když y = ln(x), pak x = exp(y) = ey.
Platí ln(exp(x)) = x, exp(ln(x)) = x.
Příklad 4.2.E - přirozený logaritmus
// Vypočítáme ln(3.5)
log(3.5)
ans = 1.252763
log([1 2 3])
ans =
0. 0.6931472 1.0986123
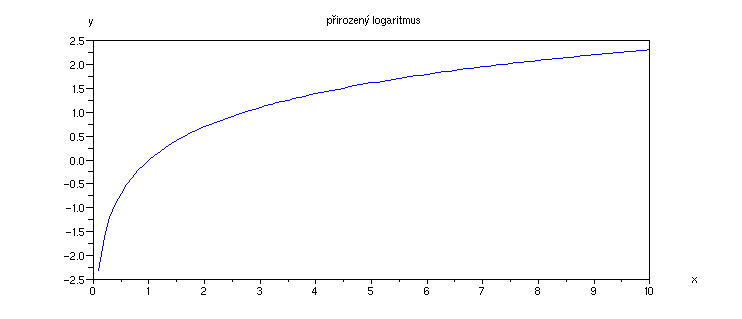
Graf log(x) vykreslíme v rozmezí 0 < x < 10 (není definován pro hodnoty x <= 0)
Příklad 4.2.F - graf přirozeného logaritmu
x = [0.1:0.1:10]; // definujeme obor hodnot x
plot(x,log(x)); // graf
xtitle('přirozený logaritmus', 'x','y') // popis grafu a os
| Syntaxe: |
y=log10(x)
y=log2(x)
|
Kromě přirozeného logaritmu log(x) Scilab poskytuje funkce log10(x) a log2(x), které vypočítají logaritmy se základem 10 nebo 2. Tyto funkce se používají velmi podobně jako funkce log(x).
Příklad 4.2.G - funkce log10 a log2
// log10 x
log10([100 200 1000 1500])
ans =
2. 2.30103 3. 3.1760913
// log2 x
log2([8 23 256 1000])
ans =
3. 4.523562 8. 9.9657843
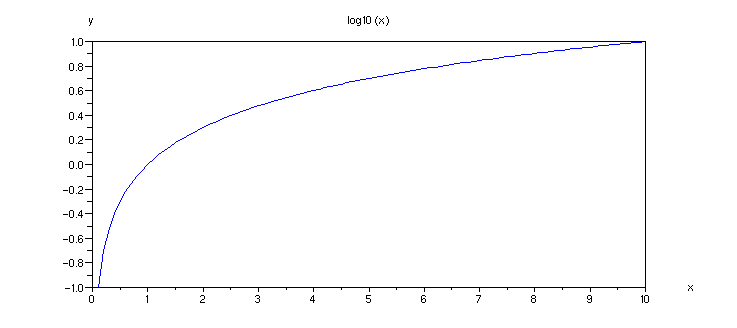
Můžeme si vykreslit grafy těchto funkcí:
Příklad 4.2.H - graf funkce log10
x = [0.1:0.1:10]; // definujeme obor hodnot x
plot(x,log10(x)); // graf
xtitle('log10 (x)', 'x','y')// popis grafu a os
Příklad 4.2.I - graf funkce log2
x = [0.1:0.1:10]; // definujeme obor hodnot x
plot(x,log2(x)); // graf
xtitle('log2 (x)', 'x','y') // popis grafu a os
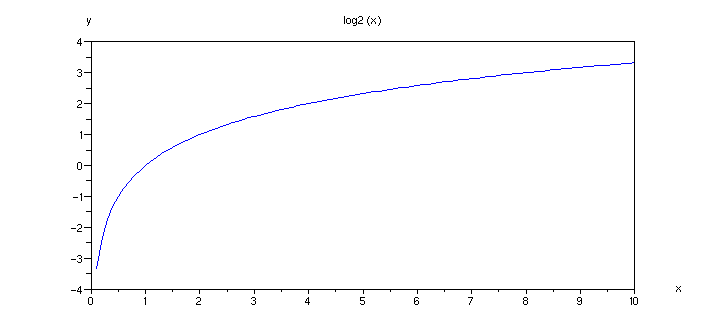
Na první pohled se nám všechny tři křivky zdají stejné, ale zkusme si je zobrazit do jednoho grafu:
Příklad 4.2.J - grafy funkcí log10 a log2 v jednom grafu
x = [0.1:0.1:10]; // definujeme obor hodnot x
plot(x,log(x),'b', x,log10(x),'r', x, log2(x), 'g') // graf
xtitle('log2 (x)', 'x','y') // popis grafu a os
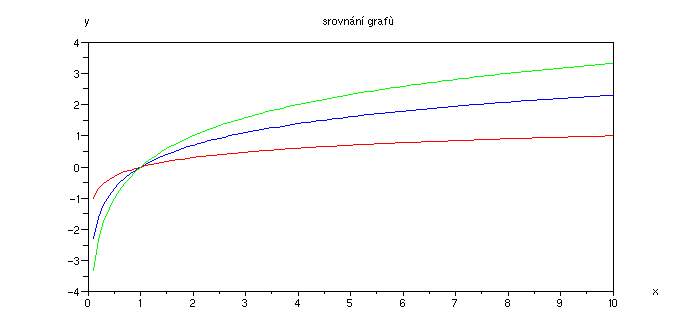
Inverzní funkce k logaritmu o základu a loga(x) je exponenciála ax.
Platí loga(ax) = x , alogax = x.
Grafy těchto funkcí:
Příklad 4.2.K - graf exponenciály 10^x
x = [-1:0.1:2]; // definujeme obor hodnot x
plot(x,10^x); // graf
xtitle('graf 10^x', 'x','y') // popis grafu a os
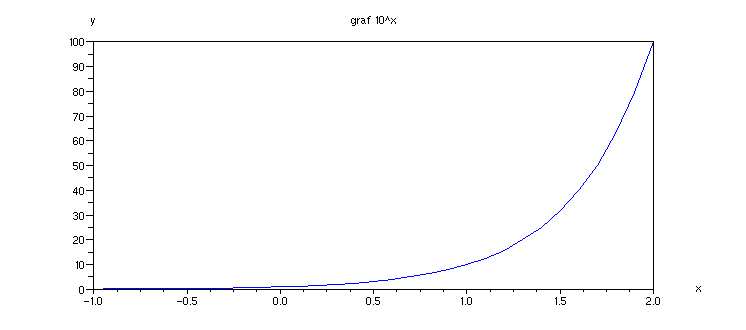
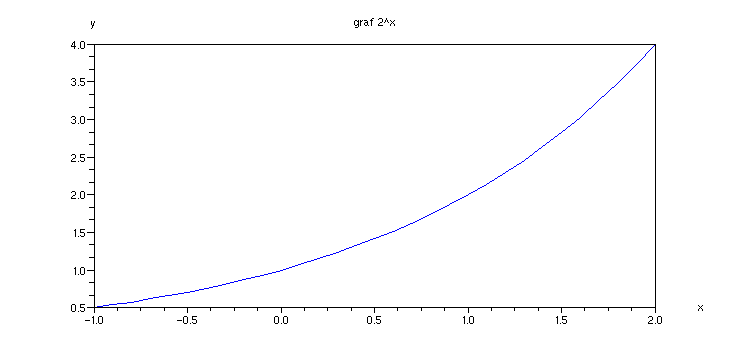
Příklad 4.2.L - graf exponenciály 2^x
x = [-1:0.1:2]; // definujeme obor hodnot x
plot(x,2^x); // graf
xtitle('graf 2^x', 'x','y') // popis grafu a os