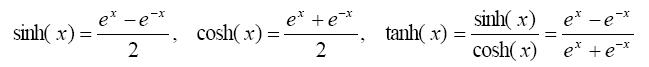Goniometrické funkce
Mezi základní goniometrické funkce patří sinus (sin), kosinus (cos), tangens (tan), kotangens (cotg). Tyto funkce jsou definovány pomocí stran a úhlů v pravoúhlém trojúhelníku.

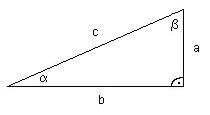sin(a)= a/c cos(a)= b/c
tan(a)= a/b cotg(a)= b/a


Ve Scilabu jsou předdefinovány čtyři goniometrické funkce (sin, cos, tan, cotg) a tři inverzní funkce arkus sinus (asin), arkus kosinus (acos) a arkus tangens (atan).

Funkce sin

Syntaxe: [y] = sin(x)


Příklad 4.3.A - výpočty - funkce sin
 sin([0 %pi/6 %pi/4 %pi/3 %pi/2 %pi])
 ans  = 

    0.    0.5    0.7071068    0.8660254    1.    0
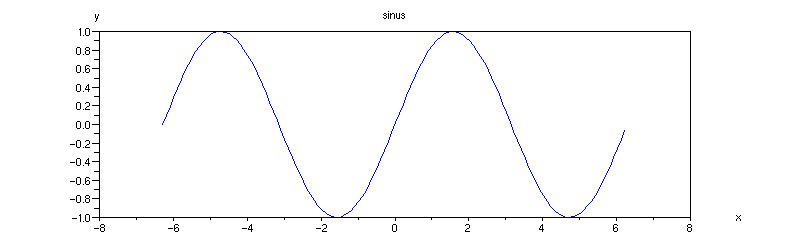
Graf funkce sin(x):

Příklad 4.3.B - graf funkce sin
 x = [-2*%pi:0.1:2*%pi];
 plot(x, sin(x));
 xtitle('sinus', 'x','y')


Funkce cos

Syntaxe: [y] = cos(x)


Příklad 4.3.C - výpočty - funkce cos
 cos[0 %pi/6 %pi/4 %pi/3 %pi/2 %pi])
 ans  =

    1.    0.8660254    0.7071068    0.5    0  - 1.
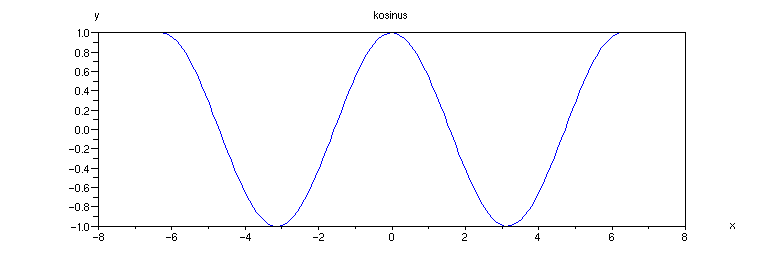
Graf funkce cos(x):

Příklad 4.3.D - graf funkce cos
 x = [-2*%pi:0.1:2*%pi];
 plot(x, cos(x));
 xtitle('kosinus', 'x','y')


Funkce tan

Syntaxe: [y] = tan(x)


Příklad 4.3.E - výpočty - funkce tan
 tan([0 %pi/6 %pi/4 %pi/3 %pi])
 ans  =

    0.    0.5773503    1.    1.7320508    0
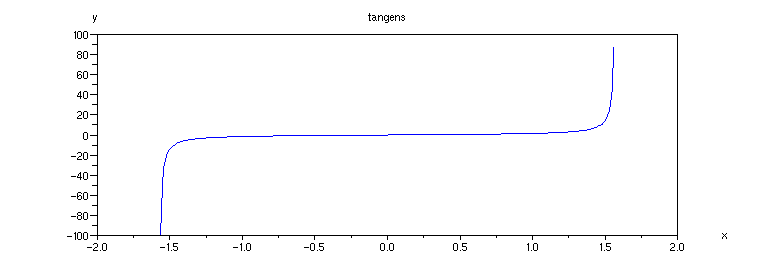
Graf funkce tan(x):

Příklad 4.3.F - graf funkce tan
 x = [-%pi/2+0.01:0.01:%pi/2-0.01];
 plot(x, tan(x));
 xtitle('tangens', 'x','y')


Funkce cotg

Syntaxe: [y] = cotg(x)


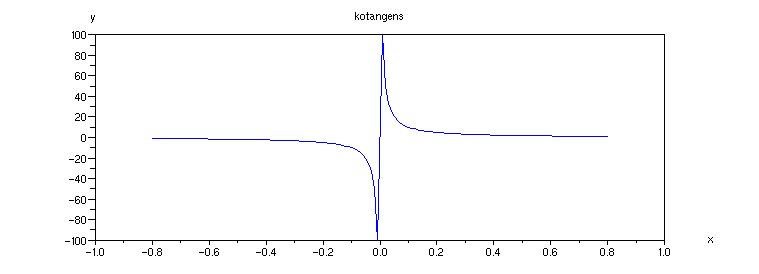
Příklad 4.3.G - graf funkce cotg
 x1 = [-0.8:0.01:-0.01]; x2 = [0.01:0.01:0.8]; x = [x1, x2];
 plot(x, cotg(x))
 xtitle('kotangens', 'x','y')




Inverzní funkce

Při vyčíslování inverzních funkcí musíme mít na paměti jejich definiční obor. Například pro sinus a kosinus je to interval [-1,1], proto funkce asin(x) a acos(x) vrací reálná čísla pouze pro interval -1 < x < 1.

Funkce asin

Syntaxe: [y] = asin(x)


Příklad 4.3.H - graf funkce asin
 x = [-1:0.01:1];
 plot(x, asin(x))
 xtitle('arkus sinus', 'x','y')


Funkce acos

Syntaxe: [y] = acos(x)


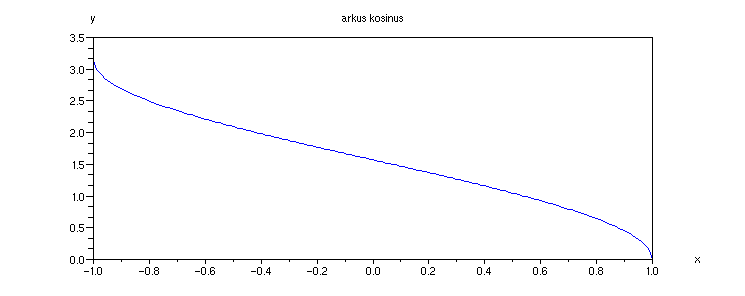
Příklad 4.3.I - graf funkce acos
 x = [-1:0.01:1];
 plot(x, acos(x))
 xtitle('arkus kosinus', 'x','y')


Funkce atan

Syntaxe: [y] = atan(x)


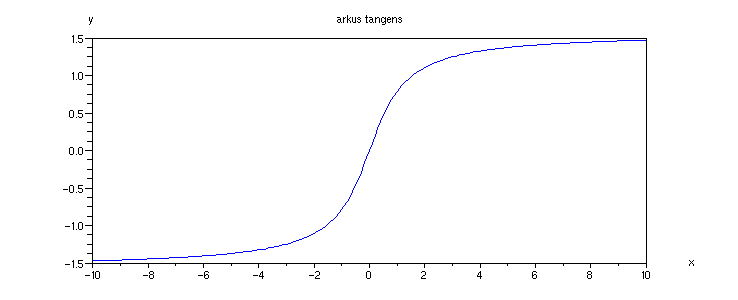
Příklad 4.3.J - graf funkce atan
 x = [-10:0.1:10];
 plot(x,atan(x));
 xtitle('arkus tangens', 'x','y')





Hyperbolické funkce

Hyperbolické funkce vycházejí z kombinace exponenciálních funkcí.
Hyperbolický sinus (sinh), hyperbolický kosinus (cosh) a hyperbolický tangens (tanh) jsou definovány:



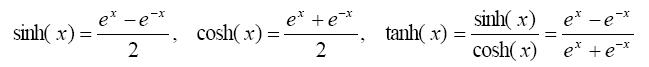
Hyperbolický kotangens je definován jako coth(x)=1/tanh(x)

K hyperbolickým funkcím existují také inverzní funkce asinh, acosh, atanh.

Funkce sinh

Syntaxe: [y] = sinh(x)


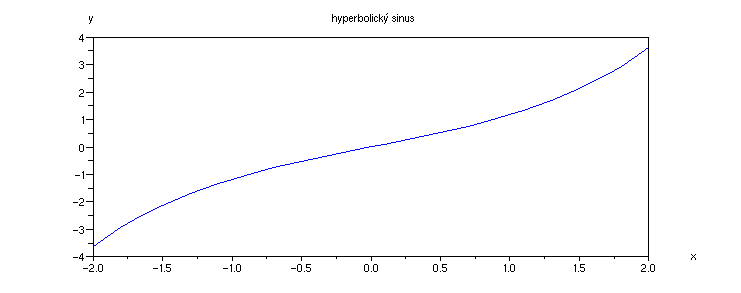
Příklad 4.3.K - graf funkce sinh
 x = [-2:0.1:2];
 plot(x,sinh(x));
 xtitle('hyperbolický sinus', 'x','y')


Funkce cosh

Syntaxe: [y] = cosh(x)


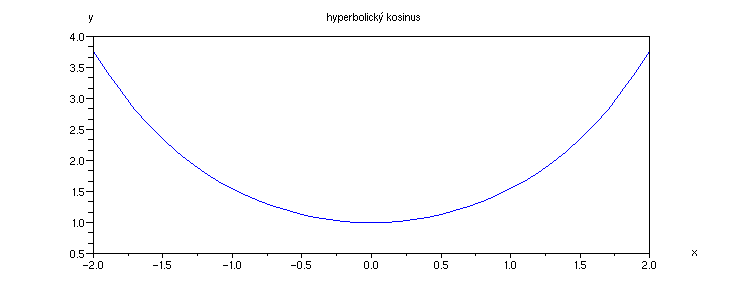
Příklad 4.3.L - graf funkce cosh
 x = [-2:0.1:2];
 plot(x,cos(x));
 xtitle('hyperbolický kosinus', 'x','y')


Funkce tanh

Syntaxe: [y] = tanh(x)


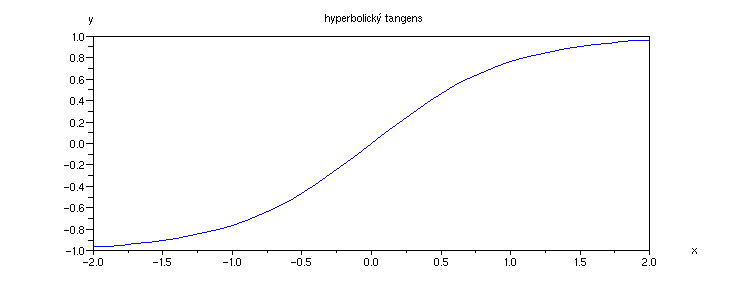
Příklad 4.3.M - graf funkce tanh
 x = [-2:0.1:2];
 plot(x,tanh(x));
 xtitle('hyperbolický tangens', 'x','y')


Funkce coth

Syntaxe: [y] = coth(x)


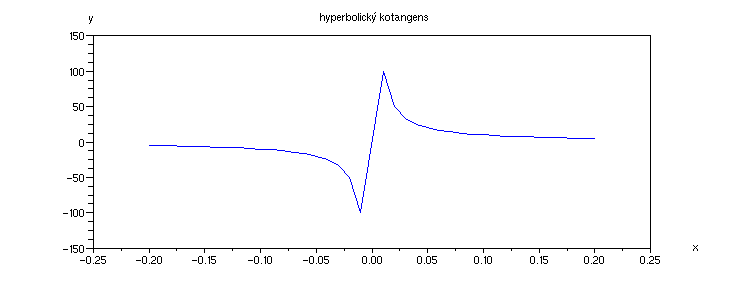
Příklad 4.3.N - graf funkce coth
 x1=[-0.2:0.01:-0.01];x2=[0.01:0.01:0.2];x=[x1,x2];
 plot(x,coth(x));
 xtitle('hyperbolický kotangens', 'x','y')


Funkce asinh

Syntaxe: [y] = asinh(x)


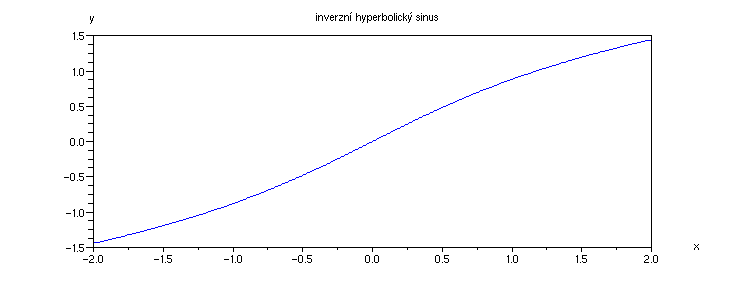
Příklad 4.3.O - graf funkce asinh
 x=[-2:0.01:2];
 plot(x,asinh(x));
 xtitle('inverzní hyperbolický sinus', 'x','y')


Funkce acosh

Syntaxe: [y] = acosh(x)


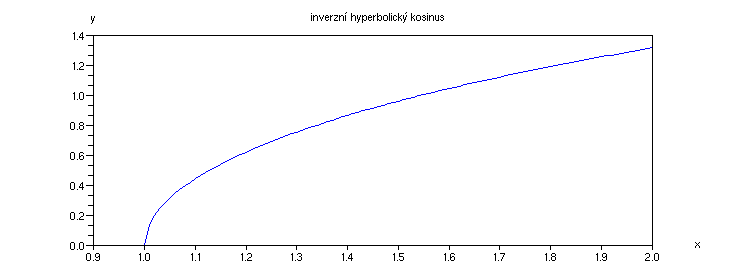
Příklad 4.3.P - graf funkce acosh
 x=[1:0.01:2];
 plot(x,acosh(x));
 xtitle('inverzní hyperbolický kosinus', 'x','y')


Funkce atanh

Syntaxe: [y] = atanh(x)


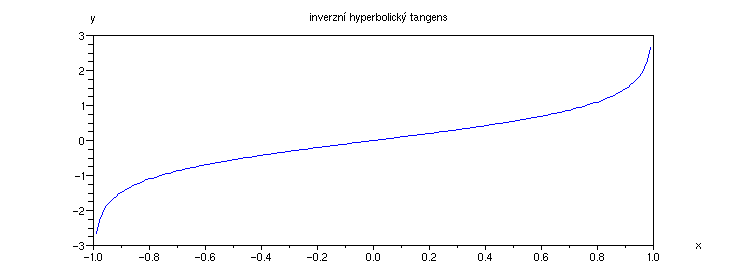
Příklad 4.3.Q - graf funkce atanh
 x=[-0.99:0.01:0.99];
 plot(x,atanh(x));
 xtitle('inverzní hyperbolický tangens', 'x','y')