Funkce pro práci s čísly
| Syntaxe: |
[B] = clean(A [epsa])
|
kde A je matice a parametr epsa je velmi malé reálná čísla (default hodnota je 1.d-10). Funkce clean zaokrouhlí malá čísla k nule pro absolutní hodnoty menší než epsa
Pro ukázku použití funkce clean vytvoříme matici A o rozměru 3x3 a vynásobíme ji její inverzní maticí.
Příklad 4.1.A - funkce clean
A = [1,3,2;-1,2,1;4,2,1] // matice A
A =
1. 3. 2.
- 1. 2. 1.
4. 2. 1.
Vypočítáme B = A×A-1, která vytvoří jednotkovou matici 3x3:
B = A*inv(A) // matice B
B =
1. - 3.053D-16 - 8.327D-17
0 1. - 2.776D-17
1.110D-16 - 3.331D-16 1.
Hodnoty prvků pod a nad diagonálou by měly být nulové, ale díky drobným numerickým chybám při výpočtu inverzní matice jsou některé hodnoty pouze blížící se k nule. Funkce clean tato velmi malá čísla "vyčistí" (zaokrouhlí na nulu), takže dostaneme požadovanou jednotkovou matici s nulami mimo hlavní diagonálu.
B = clean(B) // matice B - jednotková matice
B =
1. 0. 0.
0. 1. 0.
0. 0. 1.
kde funkce ceil(x) zaokrouhluje nahoru k celému číslu.
Příklad 4.1.B - funkce ceil
ceil(1.2) // zaokrouhluje nahoru
ans = 2
ceil(-1.2) // zaokrouhluje nahoru
ans = - 1
kde funkce floor(x) zaokrouhluje dolů k celému číslu.
Příklad 4.1.C - funkce floor
floor(1.2) // zaokrouhluje dolů
ans = 1
floor(-1.2) // zaokrouhluje dolů
ans = - 2
kde funkce round(x) zaokrouhluje nahoru nebo dolů podle matematických pravidel.
Příklad 4.1.D - funkce round
round([1.25 1.50 1.75]) // zaokrouhluje nahoru nebo dolů
ans =
1. 2. 2.
Funkce fix(x) číslo za desetinnou čárkou zaokrouhlí k nule.
Příklad 4.1.E - funkce fix
fix([1.25 1.50 1.75]) // zaokrouhluje dolů
ans =
1. 1. 1.
Funkce int(x) vrací celou část čísla.
Za povšimnutí stojí, že funkce floor a fix zaokrouhlují dolů k nejbližšímu celému číslu, jejich výsledek tedy bude stejný s funkcí int.
Příklad 4.1.F - funkce int
int([-1.2 1.2 2.3]) // celočíselná část
ans =
- 1. 1. 2.
// desetinnou část čísla dostaneme tak,
že odečteme od desetinného čísla jeho celočíselnou část
x = 12.4345;
x-int(x)
ans = .4345
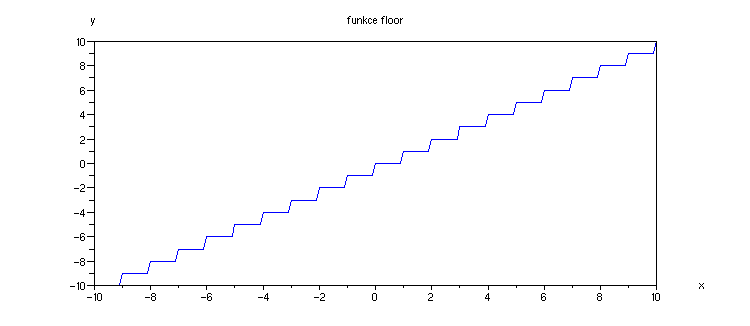
Dále si vykreslíme graf funkce floor a ceil:
Příklad 4.1.G - graf funkce floor
x = -10:0.1:10;
plot(x,floor(x))
xtitle ('funkce floor','x', 'y')
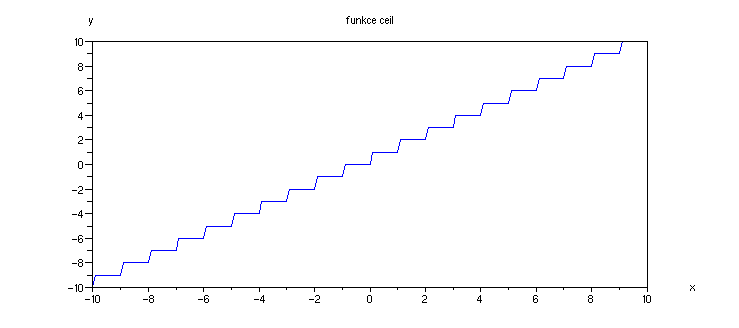
Funkce ceil je velmi podobná funkci floor:
Příklad 4.1.H - graf funkce ceil
x = -10:0.1:10;
plot(x,ceil(x))
xtitle ('funkce ceil','x', 'y')
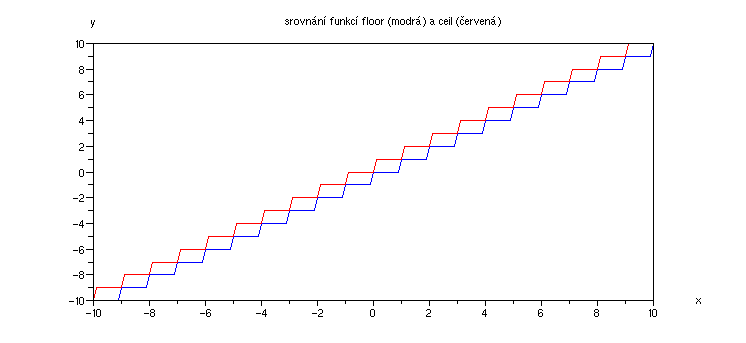
Jen pro srovnání si můžeme vykreslit oba grafy do jednoho okna:
Komplexní čísla
Funkce clean, ceil, floor, fix, int, a round můžeme použít i u komplexních čísel. V tomto případě je funkce aplikována na reálnou a imaginární část jednotlivě.
Příklad 4.1.I - komplexní čísla
z = 2.3 - 5.2*%i // definice komplexního čísla z
z = 2.3 - 5.2i
ceil(z)
ans = 3. - 5.i
floor(z)
ans = 2. - 6.i
int(z)
ans = 2. - 5.i
round(z)
ans = 2. - 5.i
fix(z)
ans = 2. - 5.i
Komplexní číslo se píše ve tvaru z = a + bi, kde a a b jsou reálná čísla a i = (-1)^(1/2) je imaginární jednotka.
a je reálná část z, a = Re(z)
b je imaginární část z, b = Im(z)
| Syntaxe: |
[y] = real(x)
[y] = imag(x)
|
Pomocí funkcí real a imag můžeme získat reálnou a imaginární část komplexního čísla.
Tady je příklad použití těchto funkcí:
Příklad 4.1.J - funkce real a imag
z = 2.4 + 3.5*%i // definice komplexního čísla z
z = 2.4 + 3.5i
x = real(z)
x = 2.4
y = imag(z)
y = 3.5
Funkce abs (x) vrací absolutní hodnotu čísla.
U komplexních čísel je absolutní hodnota definována jako |z| = sqrt (a^2 + b^2)
Příklad 4.1.K - funkce abs
abs ([-3.4 0.0 3.4]) // absolutní hodnoty reálných čísel
ans =
3.4 0. 3.4
abs (-3 + 4*%i) // absolutní hodnota komplexního čísla
ans = 5.
Funkce sign(A) vrací hodnotu 1.0, -1.0 nebo 0.0 pro reálná čísla podle toho jestli je číslo kladné, záporné nebo nula. Nazývá se také znaménková funkce.
Pro komplexní čísla vrací funkce sign hodnotu z/|z|.
Příklad 4.1.L - funkce sign
sign([-2.4 0.0 5.8]) // pro reálná čísla
ans =
- 1. 0. 1.
sign(3-4*%i) // pro komplexní čísla
ans = 0.6 - 0.8i
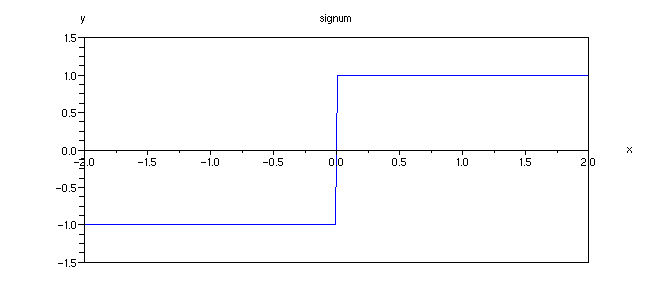
Jednoduché znázornění funkce signum pomocí grafu:
Příklad 4.1.M - graf funkce sign
x=[-2:0.1:2]; // definujeme obor hodnot x
plot(x,sign(x)); // graf
xtitle('signum', 'x', 'y') // popis grafu a os
Funkce modulo(n, m) se používá pro výpočet zbytku při celočíselném dělení. Při volání funkce ve tvaru modulo (n,m) se vypočítá číslo n - m * int (n / m),
kde n,m jsou reálná čísla.
Příklad 4.1.N - funkce modulo
modulo(10,7)
ans = 3.
// je stejné jako
10-7*int(10/7)
ans = 3.
Funkci modulo můžeme také použít při ověřování dělitelnosti dvou celých čísel - číslo n je násobek čísla m, když modulo(n,m) = 0
Příklad 4.1.O - funkce modulo - ověření dělitelnosti
// Je číslo 1771 dělitelné 7 ?
modulo(1771,7)
ans = 0 // ano
// Je číslo 268 dělitelné 6 ?
modulo(268,6)
ans = 4. // ne
kde x je desetinné číslo, n,d jsou celá čísla.
Funkce rat převede desetinné číslo na zlomek.
Platí: x » n/d.
Příklad 4.1.P - funkce rat
// převedeme číslo pi = 3.14159 na zlomek
[n,d] = rat(3.14159)
d = 113.
n = 355.
// ověříme výsledek
n/d
ans = 3.1415929
Funkce sqrt(x) vypočítá druhou odmocninu čísla. Druhá odmocnina kladného reálného čísla je kladné reálné číslo. Odmocnina záporného čísla je komplexní číslo.
Příklad 4.1.Q - funkce sqrt
// druhá odmocnina kladného čísla
sqrt(561.69)
ans = 23.7
// druhá odmocnina záporného čísla
sqrt(-2355.1609)
ans = 48.53i
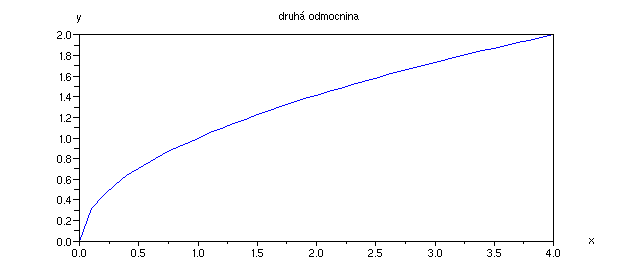
Graf druhé odmocniny můžeme vykreslit pouze pro kladná čísla x > 0:
Příklad 4.1.R - graf druhé odmocniny
x=[0:0.1:4]; // definujeme obor hodnot x
plot(x,sqrt(x)); // graf
xtitle('druhá odmocnina', 'x', 'y') // popis grafu a os
Pro výpočet faktoriálu slouží funkce gamma(x), která je definována jako n! = gamma(n+1)
Příklad 4.1.S - faktoriál
// Vypočítáme 5!
gamma(5+1) // nebo můžeme napsat přímo gamma(6)
ans =
120.
Vygenerujeme si faktoriál pro hodnoty 1 až 10:
Příklad 4.1.T - faktoriál pro hodnoty 1 až 10
x = [1:10]'; // vektor s hodnotami 1 až 10
fakt = [x, gamma(x+1)]
fakt =
1. 1.
2. 2.
3. 6.
4. 24.
5. 120.
6. 720.
7. 5040.
8. 40320.
9. 362880.
10. 3628800.