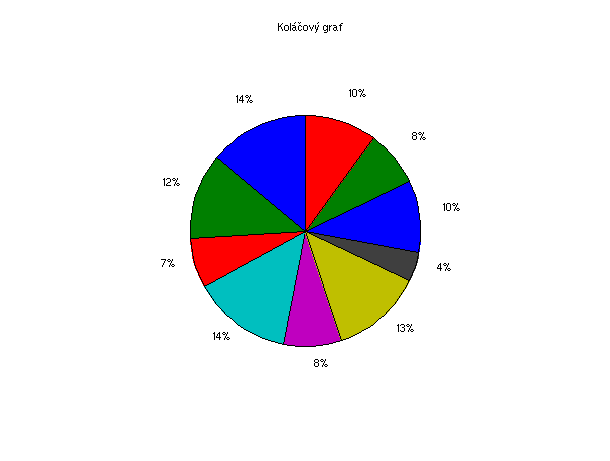Speciální grafy
Histogram
Sloupcový diagram neboli histogram se používá ke znázornění četností dat v matematické statistice. Hodnoty znaku jsou sdruženy do intervalů x. Tyto intervaly tvoří základny sloupků, odpovídající četnosti pak udávají jejich výšky.
| Syntaxe: |
histplot(x, data,< opt_args>)
|
kde x udává počet intervalů, data je soubor (matice)dat, například celých čísel. Položka opt_args jsou volitelné parametry a jejich zápis je stejný jako u funkce plot2d.
Příklad: vygenerujeme 100 celých čísel v intervalu od 0 do 100 a určíme jejich četnost pomocí grafu. Vygenerovanou matici čísel můžeme pro názornost a přehlednost seřadit sestupně příkazem sort.
Příklad 5.4.3.A - histogram
d=int(rand(10,10)*101) // vygenerujeme data
histplot(20,d)
// vygenerované hodnoty mohou být třeba takové:
d =
10. 36. 82. 99. 5. 69. 80. 82. 5. 37.
42. 19. 71. 99. 57. 70. 17. 31. 71. 64.
7. 74. 47. 83. 83. 10. 87. 0. 15. 33.
39. 51. 58. 72. 27. 89. 52. 59. 39. 32.
91. 45. 92. 59. 14. 43. 18. 20. 53. 18.
27. 74. 53. 94. 25. 17. 25. 54. 36. 89.
32. 11. 34. 99. 44. 8. 33. 54. 33. 86.
63. 43. 1. 44. 51. 2. 60. 97. 31. 57.
29. 49. 9. 7. 15. 75. 100. 21. 33. 80.
4. 15. 22. 94. 3. 73. 13. 96. 10. 78.
s=sort(d) // seřadíme hodnoty
s =
100. 89. 78. 64. 53. 43. 33. 25. 15. 8.
99. 89. 75. 63. 53. 43. 33. 25. 15. 7.
99. 87. 74. 60. 52. 42. 33. 22. 15. 7.
99. 86. 74. 59. 51. 39. 32. 21. 14. 5.
97. 83. 73. 59. 51. 39. 32. 20. 13. 5.
96. 83. 72. 58. 49. 37. 31. 19. 11. 4.
94. 82. 71. 57. 47. 36. 31. 18. 10. 3.
94. 82. 71. 57. 45. 36. 29. 18. 10. 2.
92. 80. 70. 54. 44. 34. 27. 17. 10. 1.
91. 80. 69. 54. 44. 33. 27. 17. 9. 0.
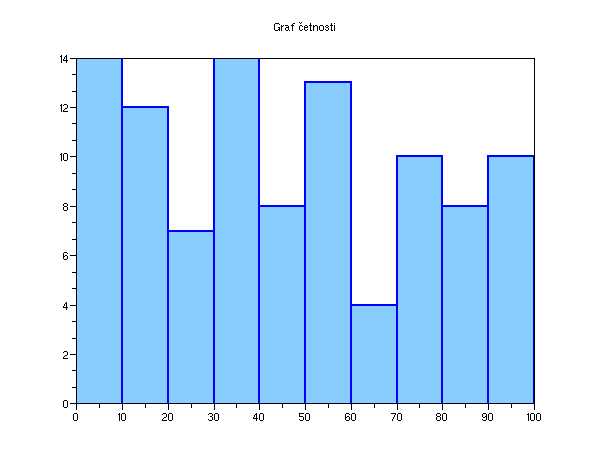
histplot(10,d)
Výsledný graf s doplněním barev potom vypadá takto:
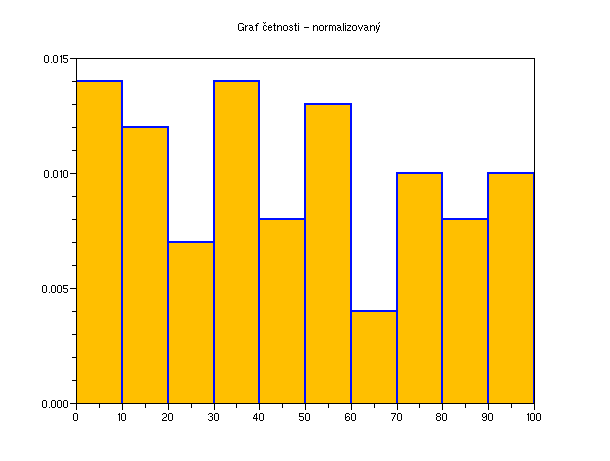
Tento graf je v normalizovaném tvaru. Pokud nechceme normalizovaný graf, stačí do parametrů grafu zapsat normalize = %f (false). Default hodnota je nastavená na %t (true).
Příklad 5.4.3.B - normalizovaný histogram
histplot(10,d, normalization = %f)
Nenormalizovaný graf:
Koláčový graf
| Syntaxe: |
pie(x)
pie(x, [sp], [txt] )
|
kde x je vektor se vstupními daty. Sp a txt je volitelná položka. Sp umožňuje vyřezání a posunutí jednoho nebo více klínů z grafu směrem od středu. Zapisuje se v podobě vektoru nul(neposunutý) a jedniček(posunutý), který musí mít stejnou velikost jako vstupní data. Txt je vektor taky o stejné velikosti jako vstupní data a dovoluje napsat text pro každou položku grafu.
Pro ukázku použijeme data z předchozího příkladu a do koláčového grafu zobrazíme četnosti.
Příklad 5.4.3.C - koláčový graf
pie([14 12 7 14 8 13 4 10 8 10])
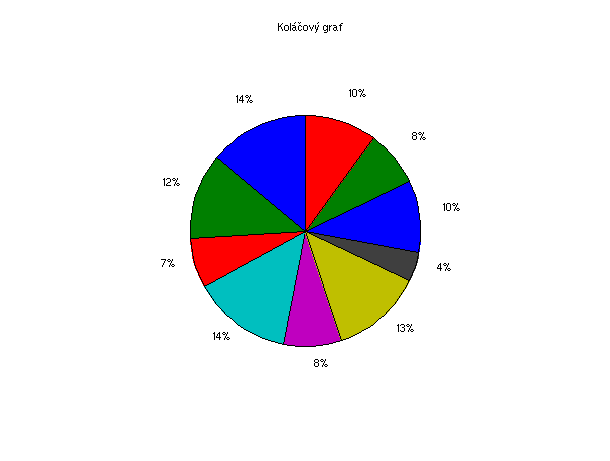
Popisek jednotlivých dílků se automaticky vytvoří v procentech. Vlastní popisek dílků můžeme zapsat přímo do příkazového řádku v položce txt, nebo pomocí grafického editoru (GED). Navíc některé dílky můžeme posunout ven (například dílky s největší četností).
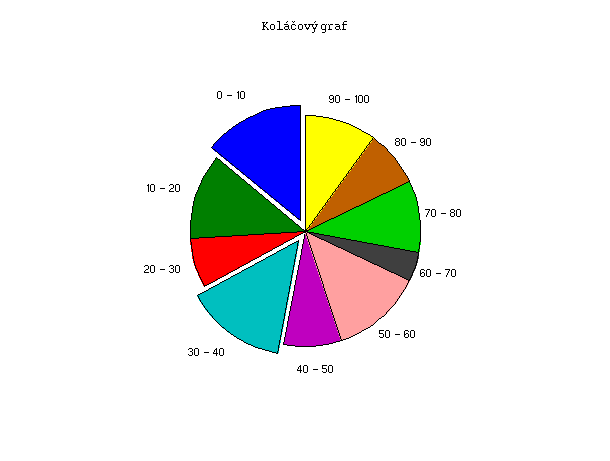
Popisky dílků uděláme pomocí grafického editoru, kde máme i možnost popisek vycentrovat (text box mode).
Příklad 5.4.3.D - upravený koláčový graf
x = [14 12 7 14 8 13 4 10 8 10];
sp = [1 0 0 1 0 0 0 0 0 0];
pie(x,sp)
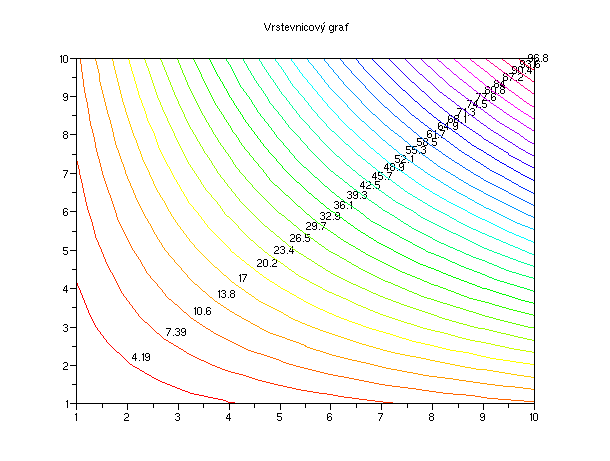
Vrstevnicový graf
Vrstevnicové grafy vykreslí hladiny křivky povrchu z=f(x,y) do 2D grafu.
| Syntaxe: |
contour2d(x, y, z, nz,< opt_args>)
|
Hodnoty f(x,y) jsou dány maticí z v mřížce bodů definovaných pomocí vektorů x a y. Nz vyjadřuje počet hladin (vrstevnic).
Téměř stejná je i funkce contourf, která jednotlivé plochy barevně vyplní.
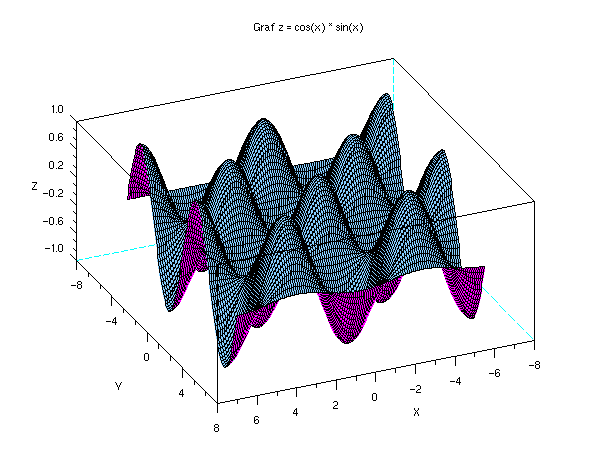
V prvním příkladu si vykreslíme do vrstevnicového grafu plochu z = cos(x)*sin(x). Nejprve obrázek této plochy ve 3D zobrazení:
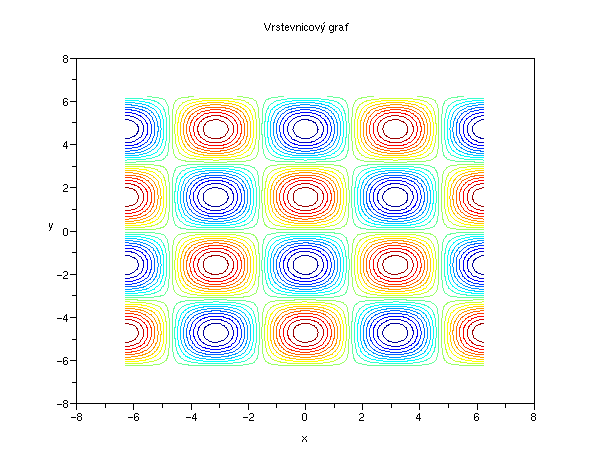
A ve vrstevnicích:
Příklad 5.4.3.E - vrstevnicový graf
f=gcf();
f.color_map=jetcolormap(20);
x = -2*%pi : 0.1 : 2*%pi;
z = cos(x')*sin(x);
contour2d(x,x,z,20);
Vrstevnicový graf vyplněný:
Příklad 5.4.3.F - vrstevnicový graf vyplněný
f=gcf();
f.color_map=jetcolormap(20);
x = -2*%pi : 0.1 : 2*%pi;
z = cos(x')*sin(x);
contourf(x,x,z,20);
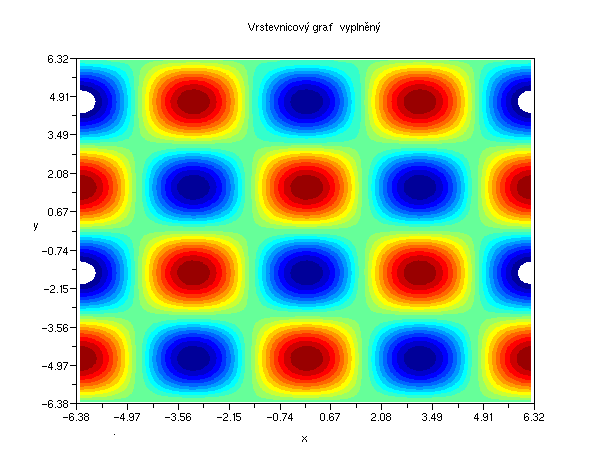
V druhém příkladu definujme jednoduchou plochu z = x*y, která vypadá takto:
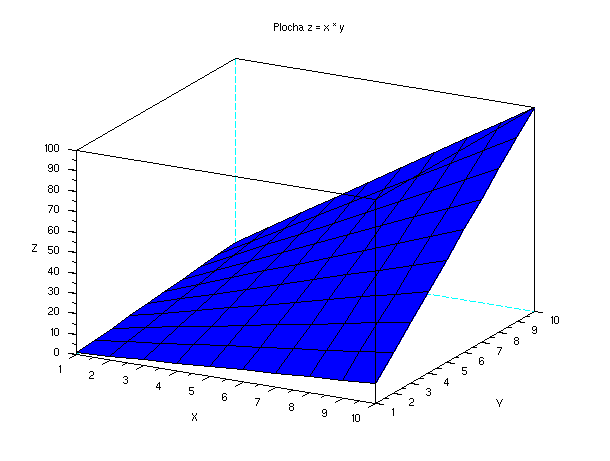
Její vrstevnicový graf:
Příklad 5.4.3.G - vrstevnicový graf plochy z = x*y
f=gcf();
f.color_map=hsvcolormap(30);
x = 1:10; y = 1:10;
z = x'*y;
contour2d(x,y,z,30); // pro vyplnění můžeme použít příkaz contourf(x,y,z,30)